Shoreline Change Analysis of Complex Shorelines
Ok, so this is not a new topic and there are some really good references/studies out there (see for example GENZ et al., 2007); however most studies deal with beach/sandy shorelines. Analysis of ‘noisy’ or complex shorelines from high resolution lidar or in wetland areas can require fairly high level data analysis to smooth out the trends. The previous studies do a great job at discussing all of the different types of data analyses – how to take the shoreline measurements and define the shoreline change trends. This is good, but maybe a bit more information on the measurement process and the description of shoreline consistency – can I measure the change differently (especially on complex shorelines) and do I recreate the same shoreline from the same data each time I digitize it or generate a shoreline from lidar - would be helpful. So I figured I would concentrate on the measurement and the assessment of shoreline consistency in this piece.
If you are doing shoreline change work there are a couple of very good shoreline change programs out there – most notably DSAS and AMBUR . DSAS runs in ArcMap and AMBUR is a standalone program running in R. Both are similar in that they are based on transects that run normal from a baseline or baselines. The geometry of the baseline is pretty/very important to both of these techniques as the ‘casting’ of transects are controlled by the alignment – to a large degree – of the baseline. Typically they are normal to the baseline. This is not a big problem on most wave dominated sandy shorelines where the baseline is pretty easy to construct, but baselines on complex bay, human influenced, or marsh shorelines can be difficult to define so as to keep transects consistent (not crossing or heading in weird directions) and cover the range of shoreline locations – some that may be curvilinear now, but were not in the past. There is some room in each of these programs for tuning transects but this can be manually intensive. I was faced with this problem on a project I recently completed where all the shorelines were either marsh, human-influenced, or complex semi-natural ones (Figure 1), so I figured it was time to try a different mouse-trap.
Figure 1. Complex shorelines and the baseline (red) used to measure the change
The technique I went with is similar to conventional transects but instead of transects being defined by the baseline alignment they are based on the shortest distance from the baseline to the shoreline (Figure 2). An analogy would be dropping a person off a vessel at each baseline node (every 10 m in my recent project) and asking them to swim the shortest distance to shore and then measuring how far they swam. I call it a “node to node” technique but that is just an unofficial name. I know someone else has used it – since in the help discussions someone asked about doing shorelines with this tool. The tool I used was run in Quantum GIS and is a QGIS algorithm called “Distance to Nearest Hub”.
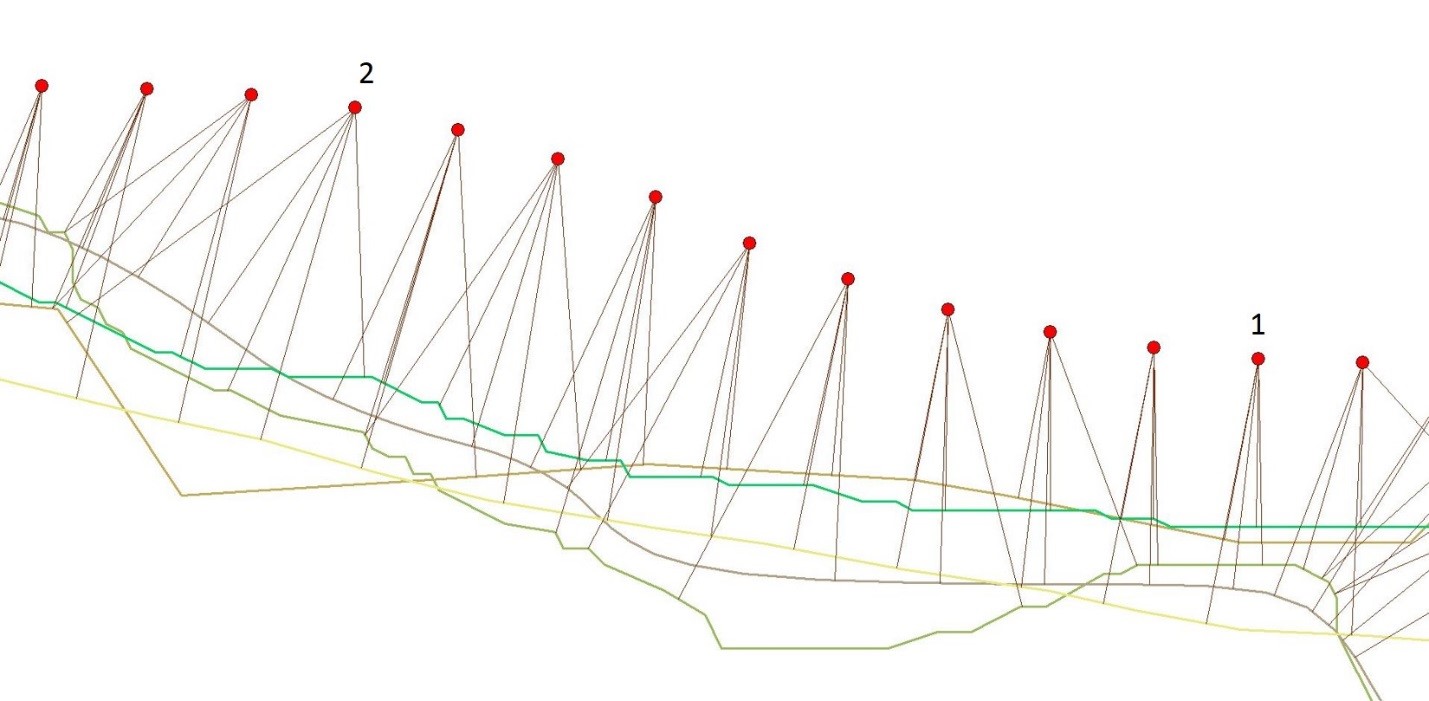
Figure 2. A small area of shoreline - 150 m - showing the nearest node technique. Note that the more complex the shoreline change (#2) the more it deviates from a ‘traditional’ transect; in sections with uniform change (#1) the analysis begins to approximate a traditional transect.
In my study area the advantages include more consistent shoreline comparison where change does not happen uniformly like in marsh dominated shorelines (Figure 1), where change often occurs chaotically (e.g., calving of a small area to form small headlands). The technique also tends to smooth out the data through time – removing noisy shoreline positions (i.e., differences in shoreline locations caused by errors in data and digitization – see below) and is a conservative estimator – again looking for the shortest distance to shore from the baseline. In this way the measurement itself is somewhat like a trend analysis. The drawbacks, however, are that the it does remove small scale changes that are real and does not show site specific change that a fixed transect would. The results, however, are much more spatially consistent and you don’t typically get spurious (or noisy) values alongshore (Figure 3).
Figure 3. Results from node to node analysis in a complex shoreline change location
Given the resolution limitations and positional errors in most historic aerials and the overall goal of showing trends, a level of smoothing and conservative estimation can be advantageous in some studies. For example, if a groin (or other sediment trapping feature) existed at the location of a transect – a couple of feet of imagery offset could cause a huge difference (noisy data) in shoreline change calculations. Using a node to node technique the difference would be minimal. So if you are working on a complex shoreline or are overwhelmed by the different choices in analysis techniques – there are like 15 or so – then trying to measure differently may be an option. One thing to note though is that in any of these techniques the baseline placement is still really important, so spend your extra time on making sure it is the best you can produce.
Shoreline Consistency and the Node to Node Technique
The absolute accuracy of historic shorelines from aerial imagery is difficult to determine since many areas change and photo-identifiable landmarks can be hard to find. An internal consistency check, however, provides a relative working accuracy assuming that it is done in a ‘blind’ fashion. To check the consistency of shorelines I chose several shoreline segments at random and digitized them a second time, following a period of time after completion of the final shoreline. They are done as blind as possible, having no reference to the initial shoreline. The internal consistency (Table 1) is measured between nodes of the lines, which were resampled to 2m, using the node to node technique described above and result in hundreds of data points (i.e., good for statistics). In this case the 2m node spacing limits the comparison to some degree since co-registered (i.e., same location) shoreline segments with slightly different node locations will have measurable offsets using this method – I have done it with 0.5m node spacing and the results change only slightly. The results (Table 1) provide a comparative assessment using a statistically robust amount of points and as many who have done shoreline digitization know, the level of consistency is directly related to the aerial imagery quality. It would be nice to see these kinds of accuracies reported regularly to get a feel for the amount of shoreline change that can really be examined in short term (like less than 10 years.) shoreline change studies. And in working with lidar data, I found that this is not just an aerial image thing, there is a level of variability for shorelines derived from different interpolation (i.e., tin vs. spline) of lidar or other elevation data especially in marsh areas that have low vegetation present.
The good news is that the node to node technique helps smooth these differences. Oh and another good aspect is that the amount of baseline nodes (i.e., transect spacing) is really almost unlimited – you could have a ‘transect’ every 2 m if you desired (like in the consistency check).
So, I guess I hope that the ‘take away’ is that in some studies it may be better to choose a different measurement technique to smooth the data spatially instead of afterwards with different analysis techniques. I think it would be really cool to look at this node to node technique in comparison to the transect technique and the many different data analyses to see where the differences are and which works best in the various types of shorelines. If you are interested – please get in touch, it would make a great publication.
If you are interested in seeing some results - this online mapping was done with the node technique.