In the past couple of weeks I have had several conversations about planning horizons and how models, the error associated with them, and future sea levels play out in terms of time ranges. For example, is it even worth looking beyond 2050 given the magnitude of unknowns in sea level change (SLC)? In 35 years there may be significant changes that make all the tweaking of models and talk of lidar elevation errors a moot point; then again, it may be just as we envisioned. There are no easy answers, but sometimes simple models of the concepts are a good place to start. So, given what we know about predicted sea level trends (Figure 1) and the errors associated with data and other models maybe we can squeeze out some broad boundaries.

Figure 1. Sea level change curves from NOAA and the computed average.

Mapping future SL change is, in many places, an example of a relatively straightforward model, being largely dependent on water and land elevations. Yes, when you start to look at more dynamic landforms (e.g., barrier beach systems) the picture gets significantly more complex; but for the low energy settings or where infrastructure is present, which is where most people live, the amount of morphological change is fairly limited. Using these areas as an example maybe we can begin to explore the limits of reasonable mapping.

As we all know, the predicted changes in regional (Figure 1) or local sea level become quite large as we move towards the next century. Tomorrow’s prediction, however, is pretty darn good. Lidar’s depiction of tomorrow’s elevation is not nearly as good – it is a model after all – but for those areas in low energy settings the future’s elevation prediction is probably not far off from todays. Likewise, tidal dynamics, while being affected by local changes in basin geometry, probably won’t change to any great degree in the future.

To highlight the simple time vs. uncertainty ratios I am going to use some of my recent work on sea level mapping in Massachusetts as an example. The Lidar data in the study has a RMSE for open areas of 15 cm, which I double (30 cm RMSE) for the RMSE of all areas (not just flat ones) and land covers and also the resampling of the points for DEM creation. To some an RMSE of 30 cm may seem high, however, I would rather err on the conservative side for the products developed. VDatum was used to map tidal heights (MHHW in this case) and has an MCU of 13 cm.

In this analysis, I am going to assume that these ‘elevation’ error measures approximate the standard deviations for use in Gaussian statistics. I don’t think it is really that much of a stretch since it is a conservative assumption; RMSE should be more than the stand deviation in most lidar data sets. Statistics on the SLC (Figure 1) are taken from the NOAA curves and have been discussed in an earlier blog. The standard deviation of the 4 curves varies over time, which is a very important point (!).

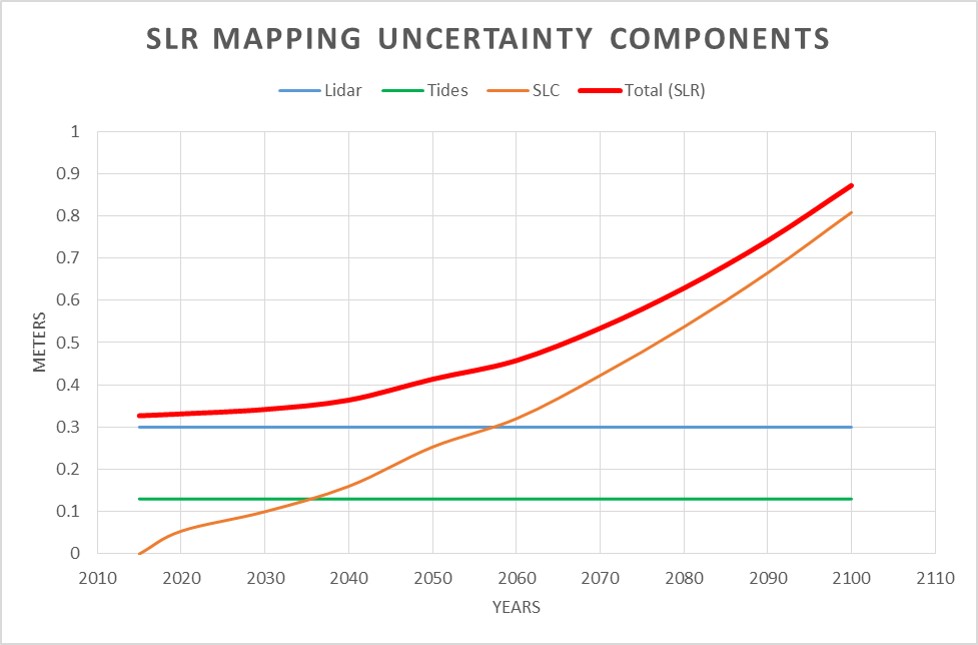
With that in mind, when we put the uncertainties of the components together (using a sum of squares to compute an MCU) the graphs (Figures 2 and 3) of uncertainty through time starts to provide clues about some important future boundaries and an idea of how the various components contribute to the overall uncertainty.

Figure 2. Error/uncertainty values through time

Figure 3. Relative error/uncertainty through time

There are a couple dates that stick out, the first being the present and that the error in determining the present MHHW is really a function of the elevation data – no surprise there – and about as good as it is going to get. Another notable time in both graphs is the period between 2050 and 2060. It is at this point (Figure 2) that the MCU starts to accelerate upward as the SLC uncertainty begins to drive the MCU and is in the 0.5 meter range. Likewise, the graph of percentages (Figure 3) shows the crossover from an elevation based uncertainty to a SLC based uncertainty in this period. Tidal errors would seem to be relative noise in the big picture beyond the present, however, this does not take into account the changes from basin variations – which could be large in some areas if some of the higher SLC scenarios happen to come to fruition.

OK, this is a simple look at how time and elevation play into mapping uncertainty; however, to me it suggests that going beyond 2060 probably contains more conjecture than prudence would dictate for resilience planning, especially when conveying this information to citizens. This also highlights, for me anyway, the ever-debated argument of mapping SLC with lidar data and what levels of change should be shown.

My take on this subject is that SLC mapping is really a time (4th dimension) exercise not a height one – we live through time not through elevation. So, if one argues, based on sound standards, that anything less than 1 foot contours should not be produced, which would equate to around 2050 based on the average of the NOAA curves (Figure 1), another could argue that anything past 2050 starts to carry significant uncertainty in its totality not just elevation wise.

Where would this leave us? I think that the point could be made that we should not use mapping as a tool in SLC. Personally, I don’t think that this is the case. Rather, to me it suggests that we should be up-front and transparent about the uncertainty. I think we all understand that the future is unknown, we just have to own up to that in our maps. And a good way to start doing this in the use and conveyance of the information that statistics provide. So, I say go ahead and map small increments of SLC because it is not going to get any better than a map of tomorrow’s MHHW.

Time vs. Elevation – Mapping the Third and Fourth Dimension